Introduction

Web programming is, in general, a business of dealing with texts. Client sends a text request and receives a text response. Processing web documents consists mostly of processing texts, often in a sophisticated way. While new methods like image search are under active development these days, it’s the text search that is the most well-known and adopted method.

Text algorithms offer different ways of efficient text representation, processing and lookup. Ternary search tree is one of the most interesting data structures in its field of knowledge, as it combines storage efficiency with fast lookups and ability to perform a prefix search. I’ll show you how this type of tree works and propose an example Ruby implementation, covered with specs.

A Pinch of Theory

I’m sure you know what a binary search tree is. Each node contains a value and references to two subtrees: first holding elements less than node value and the second, holding the greater elements. Example BST looks like this:

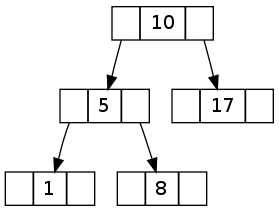
Ternary search tree is only slightly more complicated. In addition to BST, it has a third pointer in each node. When traversing a tree, this pointer should be used when value being compared is equal to the one kept in node. It’s really simple: left, right and equal pointers. Let’s take a look at an example:

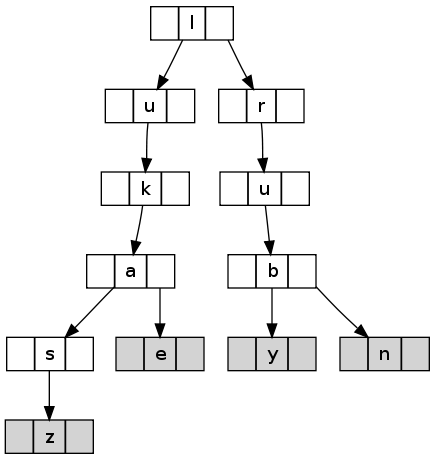
TST above was created by inserting words: “lukasz”, “luke”, “ruby” and “run” into it. Filled rectangle means that a word ends in this node. As you can see, TST keeps strings in a memory-efficient way, with minimum overhead. That is, common prefix (e.g. “luk” in “luk-asz” and “luk-e”) is stored only once.

Implementation

Let’s start implementation of ternary search tree with the search() method:

def search(string)
  return false unless (string && !string.empty? && self.value)

  head, tail = string.partition

  if head < self.value
    return @left.search(string) if @left
  elsif head == self.value
    return true if !tail && self.ending?

    return @equal.search(tail) if @equal
  elsif head > self.value
    return @right.search(string) if @right
  end
end

At the beginning, there is some defence logic. Next, string being searched for becomes partitioned into head (first character) and tail (the rest); it is a concept which I borrowed from functional programming. I hope you admit that dividing string into head and tail is much more readable then dealing with indexes (if index + 1 < string.length and so on). Partitioning procedure can be implemented like this:

# Author::    Lukasz Wrobel
# Url::       http://lukaszwrobel.pl/
class String
  def partition
    [head, tail]
  end

  # First character.
  def head
    (self.length >= 1) ? self[0].chr : nil
  end

  # Cut the first character from the string and return the tail.
  def tail
    (self.length >= 2) ? self[1..-1] : nil
  end
end

I hope this code doesn’t require any explanation, it’s pretty simple. Let’s get back to the search() method then. After partitioning the string, decision is made whether to proceed to the left, equal or right subtree. The second case (proceed to the equal subtree) is most interesting, as it is the only way to confirm that string is actually kept in the tree. String is found when the following condition:

!tail && self.ending?

is met. !tail means that the whole string is “spent” - there is no tail left. self.ending? checks if there is any word that ends in this place. Without marking the end, we could receive false positive results. Imagine that tree holds only the word “lukasz” and we are searching for “luk”. Without checking whether any word ends in the “k” node, we could erroneously think we found something - there is no tail and !tail evaluates to true. But the self.ending? part of the condition forces us to get rid of illusions - there is no “luk” word in the tree. By the way, this situation is covered in specs which I’ll show to you later on.

The insert() method is very similar in its concept to the search() method. Surprisingly or not, the “equal” part is the most important one:

...
elsif head == self.value
  if tail
    @equal = Tst.new unless @equal
    @equal.insert(tail)
  else
    self.ending_here()
  end
...

If there is a tail, the insertion process should be carried on. If there is none, the whole process should be stopped and the only thing left to do is marking that a word ends here.

Whole Tst class looks like this:

require 'core_ext/string'

# Author::    Lukasz Wrobel
# Url::       http://lukaszwrobel.pl/
class Tst
  def initialize
    @left = @equal = @right = nil
    @ending = false
  end

  def insert(string)
    raise ArgumentError unless string.is_a?(String)

    head, tail = string.partition

    if self.value.nil? # self.value ?
      self.value = head # self.value ?
    end

    if head < self.value
      @left = Tst.new unless @left
      @left.insert(string)
    elsif head == self.value
      if tail
        @equal = Tst.new unless @equal
        @equal.insert(tail)
      else
        self.ending_here()
      end
    elsif head > self.value
      @right = Tst.new unless @right
      @right.insert(string)
    end
  end

  def search(string)
    return false unless (string && !string.empty? && self.value)

    head, tail = string.partition

    if head < self.value
      return @left.search(string) if @left
    elsif head == self.value
      return true if !tail && self.ending?

      return @equal.search(tail) if @equal
    elsif head > self.value
      return @right.search(string) if @right
    end
  end

  alias :<< :insert
  alias :[] :search

  protected
  def value
    @value
  end

  def value=(value)
    raise ArgumentError unless acceptable?(value)

    @value = value
  end

  def acceptable?(value)
    value.is_a?(String) && value.length == 1
  end

  def ending_here
    @ending = true
  end

  def ending?
    @ending
  end
end

As you may have guessed, the core_ext/string file required at the very beginning is the one responsible for doing the partitioning business. Example session with the Tst class may look like this:

>> tst = Tst.new
>> tst << 'lukasz'
>> tst << 'ruby'

>> tst['lukasz']
=> true
>> tst['luk']
=> false

search() and insert() methods are aliased with [] and <<, respectively. Thanks to it, the Tst class can be used in a more Ruby-like way.

Specs

As usual, I decided to write some specs to cover the ternary search tree code, especially because dealing with data structures is always a little bit tricky. First spec file covers the extensions I’ve made to the core String class:

require 'core_ext/string.rb'

#
# String#head
#
describe String do
  it 'empty string: there is no head' do
    ''.head.should be_nil
  end

  it 'one-character string: the only character is the head' do
    'f'.head.should == 'f'
  end

  it 'long string: first character is the head' do
    'lukasz'.head.should == 'l'
    ('dfg' * 100).head.should == 'd'
  end
end

#
# String#tail
#
describe String do
  it 'empty string: there is no tail' do
    ''.tail.should be_nil
  end

  it 'one-character string: there is no tail' do
    'l'.tail.should be_nil
  end

  it 'two-character string: there is a one-character tail' do
    'lu'.tail.should == 'u'
  end

  it 'long string: tail - all characters in order, except the first one' do
    'lukasz'.tail.should == 'ukasz'
    ('x' * 100).tail.should == 'x' * 99
  end
end

#
# String#partition
#
describe String do
  it 'empty string: no head and no tail' do
    head, tail = ''.partition

    head.should be_nil
    tail.should be_nil
  end

  it 'one-character string: a head and no tail' do
    head, tail = 'l'.partition

    head.should == 'l'
    tail.should be_nil
  end

  it 'two-character string: a head and a one-character tail' do
    head, tail = 'lu'.partition

    head.should == 'l'
    tail.should == 'u'
  end

  it 'long string: a head and a long tail' do
    head, tail = ('x' * 80).partition

    head.should == 'x'
    tail.should == 'x' * 79
  end
end

Second spec file is dedicated exclusively to the ternary search tree code:

require 'tst.rb'

describe Tst do
  before do
    @tst = Tst.new
  end

  it 'empty tree should not contain any strings' do
    @tst[''].should be_false
    @tst['lukasz'].should be_false
    @tst['a' * 100].should be_false
  end

  it 'should allow to insert strings only' do
    [123, {}, [5, 6, 7]].each do |wrong|
      lambda {@tst << wrong}.should raise_error ArgumentError
    end
  end

  it 'should be able to find strings after inserting them' do
    @tst << 'lukasz'
    @tst['lukasz'].should be_true
  end

  it 'should not find strings that were not inserted' do
    @tst << 'lukasz'
    @tst['wrobel'].should be_false
  end

  it 'should not find strings if only a prefix does match' do
    @tst << 'lukasz'
    @tst['luk'].should be_false
  end

  it 'should not find strings if they are longer than found prefix' do
    @tst << 'lukasz'
    @tst['lukaszz'].should be_false
  end

  it 'should be able to form a simple, one-node tree' do
    @tst << 'l'
    @tst['l'].should be_true

    @tst[''].should be_false
    @tst['u'].should be_false
  end

  it 'should hold many strings at the same time' do
    @tst << 'lukasz'
    @tst << 'wrobel'
    @tst << 'ruby'
    @tst << 'rubyist'
    @tst << 'luke'

    @tst['rubyist'].should be_true
    @tst['lukasz'].should be_true
    @tst['wrobel'].should be_true
    @tst['luke'].should be_true
    @tst['ruby'].should be_true

    @tst[''].should be_false
    @tst['nonsense'].should be_false
    @tst['lukasz!!!1!!'].should be_false
  end

  it 'should have interchangeable insert and search API' do
    tst = Tst.new
    tst << 'lukasz'
    tst['lukasz'].should be_true

    tst = Tst.new
    tst.insert('lukasz')
    tst.search('lukasz').should be_true
  end
end

To bind the specs together, I used a simple Rake RSpec task I’ve mentioned some time ago:

require 'rubygems'
require 'spec/rake/spectask'

$: << File.expand_path(File.dirname(__FILE__) + "/lib")

Spec::Rake::SpecTask.new(:spec) do |t|
  t.spec_files = Dir.glob('spec/**/*_spec.rb')
  t.spec_opts << '--format specdoc'
  t.rcov = true
end

I’ve tweaked the original Rake task by adding the

$: << File.expand_path(File.dirname(__FILE__) + "/lib")

line, which expands Ruby load path. It’s a simple, but powerful trick.

Having a clever rakefile, all I have to do to run the specs is to navigate to directory containing Tst files and execute the following command:

$ rake spec

All these files form a simple project with the following directory layout:

+ tst
  - rakefile
  + lib
    - tst.rb
    + core_ext
      - string.rb
  + spec
    - tst_spec.rb
    + core_ext
      - string_spec.rb

Remarks

You must know that ternary search tree suffers from node inserting order to the same extent as regular binary search tree does. That is, having a set of words to be inserted into the tree can lead to different tree shapes, depending on word inserting order. This means variable search efficiency.

This situation is similar to partitioning in quicksort algorithm. You can either shuffle input array to reduce the risk of choosing the worst order, use a selection algorithm (like median-of-medians) or even sort the array. Simple heuristics like picking a few words from input randomly, sorting them and picking the middle one as the pivot should work quite well, too. Simply, don’t insert words in order they came, as it can lead to building an (almost) degenerated tree.

Applications

So far, I haven’t told too much about practical meaning of ternary search trees. As I’ve said before, they can be used to do fast dictionary lookups. Imagine, for example, a URL routing table. URL addresses often have a common prefix and then they branch. This is a perfect situation for TST: common prefix is stored only once, regardless of number of different URLs which branch from it. Of course, application of ternary search trees is limited in situations where regexp-based routing comes into play. However, number of regular expressions to match against can be preliminary limited using TST.

Another example of ternary search tree application is prefix matching. Imagine text input field combined with suggestion tool, which is so often adopted these days. Writing such a suggestion tool will be much more easier with a TST. Just follow the user input, visit the corresponding node and check which words can you reach from it. For example, “comput” can lead to “computer”, “computational”, “computability” and so on.

TST can also be used to do a near-neighbor search, which can be used to find words located within given distance. In other words, TST will make finding similar words effective. Such a thing couldn’t be achieved if all words were stored in a hashtable.

Summary

Ternary search tree has many practical applications and it suits well the web environment. I’ve shown you an example implementation of TST, which you can use to further extend the tree or use it in your own programs. I hope this article will encourage you to take a deeper look at some text algorithms. Believe me - there is more for text storage than just hashtables.